ST表

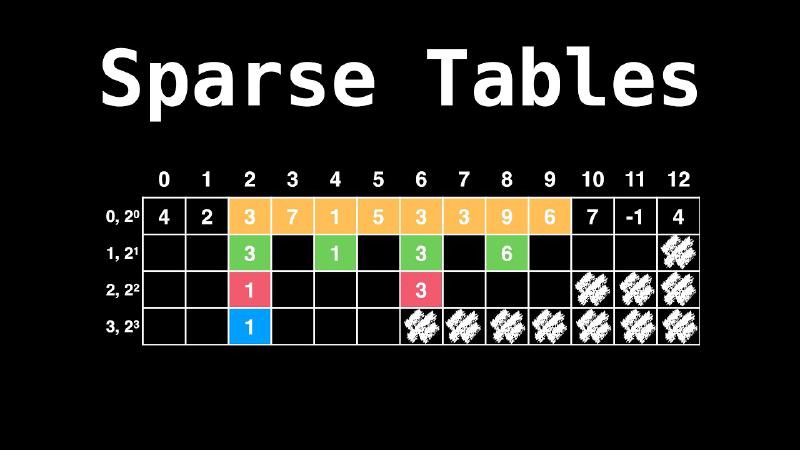
简介

可重复贡献问题

可重复贡献问题是对于运算$\oplus$，运算的性质满足x$\oplus$x=x，则对应的区间询问就是一个可重复贡献问题，例如：

最大值满足max(x,x)=x，最大公因数满足gcd(x,x)=x，

因此RMQ问题和GCD问题就是一个可重复贡献问题，

但是区间和就不满足这个性质，因为在求解区间和的过程中ST表采用的预处理区间会发生重叠，导致重叠部分被重复计算，

因此对于$\oplus$操作还需要满足集合律才能够使用ST表进行求解

什么是ST表？

ST表是一种基于倍增思想，用于解决可重复贡献问题的数据结构。

基于倍增的思想，ST表可以实现O(nlogn)下进行预处理，并在O(1)时间内回答每个询问。如果仅仅进行区间最值查询，ST表的效率完全吊打线段树；但是，相比于线段树，ST表并不支持修改操作，无论是单点修改还是区间修改都不支持。

ST表的应用

ST表应用最广泛的领域便是解决RMQ问题：给定n个数，m询问，对于每个询问，需要回答区间[l,r]中的最大值或最小值(可以采用两个数组同时进行处理)。

除RMQ以外，还有其它的“可重复贡献问题”。例如“区间按位和”、“区间按位或”、“区间 GCD”，使用ST 表都能高效地解决。

需要注意的是，对于“区间 GCD”，ST 表的查询复杂度并没有比线段树更优（令值域为 w，ST 表的查询复杂度为Θ(log w)，而线段树为 Θ ( log ⁡ n + log ⁡ w )，且值域一般是大于n的），但是 ST 表的预处理复杂度也没有比线段树更劣，而编程复杂度方面 ST 表比线段树简单很多。

如果分析一下，“可重复贡献问题”一般都带有某种类似 RMQ 的成分。例如“区间按位与”就是每一位取最小值，而“区间 GCD”则是每一个质因数的指数取最小值。

原理

预处理阶段

在简介中提到，ST表是基于倍增的思想，所以你首先应该知道的是，ST表是利用倍增思想来缩短时间的，

而倍增就体现在他数组的定义中：对于$f[i][j]$，指的是在区间的第 $i$ 项，向后 $2^j-1$ 个元素所包含区间的最大值，那么显然$f[i][0]=a_i$

对于i=1，我们可以画出这么一个图，其下表即为j：

那么当前i如何转移呢？已经很明显了，我们可以直接考虑将两个小区间的答案合并，即为这个大区间的值；

如图中$f[1][2]$即可由$max(f[1][1],f[3][1])$转移得到，

于是得到ST表的状态转移方程：

$f[i][j]=\max{(f[i][j-1],f[i+2^{j-1}][j-1])}$

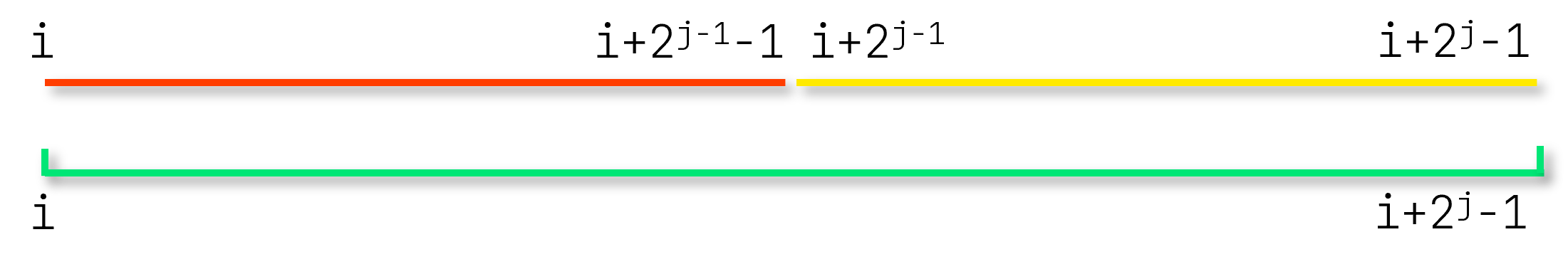
其中$2^{j-1}$在代码中可写为(1<<(j-1))的位运算形式，这样更方便也会更快。

这个方程告诉我们，ST表类似于区间DP，是由两个小区间合并上来的，

所以我们应该先枚举区间长度j，再枚举i。

状态转移到最后，一个问题应运而生了：这个转移方程有没有边界呢？

不妨来看一下i=6的例子：

可以看出在i=6时，j=3的范围是$[6,6+2^3]$即$[6,13]$，已经超出了数据的范畴（12），

所以当j=3时，i只能取到$[1,12-2^3+1]$即$[1,5]$。

由上例再根据转移方程，不难看出当j确定时，i的范围为$[1,n-2^j+1]$。

那么又根据$i=1$的情况，可知j应满足：

$2^j\le n\Leftrightarrow j\le\lg{n}$，其中$\lg{n}$表示n关于底数2的对数向下取整，可以递推求得lg[n]数组

预处理阶段的代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


void init()
{
	lg[0]=-1;
	for(int i=1;i<=n;i++)
	{
		cin>>st[i][0];
		lg[i]=lg[i>>1]+1;
	}
	for(int j=1;j<28;j++)
		for(int i=1;i+(1<<j)-1<=n;i++)
			st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}

时间复杂度为：$O(n\cdot\log_2{n})$

查询阶段

假定我们需要求区间$[l,r]$的最值，那么我们可以将该区间分成两个ST表可直接维护的小区间，然后二者求最值即可。

对于第一个区间（左端点为l），我们需要找一段ST表能在该区间内可覆盖的、最大的子区间，用数学语言描述为：

$(l+2^k-1\le R)\Leftrightarrow(k\le \lg{[r-l+1]})$，直接取等，令j=k即可，

所以第一个区间为：$f[l][k]$，其中$k=\lg{[r-l+1]}$

对于第二个区间（右端点为r），我们需要反向找一个与第一个区间要求相同的子区间，

由于对称性，k仍为第一个区间求得的$k=\lg{[r-l+1]}$

但是我们应该如何确定第二个区间的起点呢？

由于两个子区间的长度都为$2^k$，设起点在x处，则满足：

$(x+2^k-1=r)\Leftrightarrow(x=r-2^k+1)$

于是第二个区间为：$f[x][k]$，即$f[r-2^k+1][k]$

通过上述流程可以证明，两个子区间一定可以覆盖整个区间且包含于该区间，

所以不难发现答案即为：

$\max{(f[l][k],f[r-(1«k)+1][k])}$，其中$k=\lg{[r-l+1]}$

查询阶段的代码：

1
2
3
4
5


int query(int l,int r)
{
	int k=lg[r-l+1];
	return max(st[l][k],st[r-(1<<k)+1][k]);
}

时间复杂度为：$O(1)$

模板

RMQ问题

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


#include<iostream>
#include<algorithm>
#define maxn 100000001
using namespace std;
int lg[maxn];
int st[maxn][28];
int n,m;
int l,r;
void init()
{
	lg[0]=-1;
	for(int i=1;i<=n;i++)
	{
		cin>>st[i][0];
		lg[i]=lg[i>>1]+1;
	}
	for(int j=1;j<28;j++)
		for(int i=1;i+(1<<j)-1<=n;i++)
			st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
int query(int l,int r)
{
	int k=lg[r-l+1];
	return max(st[l][k],st[r-(1<<k)+1][k]);
}
int main()
{
	cin>>n>>m;
	init();
	for(int i=1;i<=m;i++)
	{
		cin>>l>>r;
		cout<<query(l,r)<<endl;
	}
}

GCD问题

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


#include<iostream>
#include<algorithm>
#define maxn 100000001
using namespace std;
int lg[maxn];
int st[maxn][28];
int n,m;
int l,r;
int gcd(int a,int b)
{
	return b?gcd(b,a%b):a;
}
void init()
{
	for(int j=1;j<28;j++)
		for(int i=1;i+(1<<j)-1<=n;i++)
			st[i][j]=gcd(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
int query(int l,int r)
{
	int k=lg[r-l+1];
	return gcd(st[l][k],st[r-(1<<k)+1][k]);
}
int main()
{
	cin>>n>>m;
	init();
	for(int i=1;i<=m;i++)
	{
		cin>>l>>r;
		cout<<query(l,r)<<endl;
	}
}

参考链接：

https://blog.csdn.net/yanweiqi1754989931/article/details/119294548

https://www.cnblogs.com/zwfymqz/p/8581995.html